26. Stokes' Theorem

Let \(S\) be a nice surface in \(\mathbb{R}^3\) with a nice properly oriented boundary, \(\partial S\), and let \(\vec{F}\) be a nice vector field on \(S\). Then \[ \iint_S \vec{\nabla}\times\vec{F}\cdot d\vec{S} =\oint_{\partial S} \vec{F}\cdot d\vec{s} \] Each piece of the boundary of the surface must be traversed counterclockwise as seen from the tip of the normal vector to the surface.

d. Applications

7. Ampere's Law

Ampere's Law is a law of physics relating electric current to the magnetic field, provided that the electric charge density is independent of time. It can be written in a differential or integral version, which are related by Stokes' Theorem. The differential version states that the curl of the magnetic field is equal to \(4\pi\) times the electric current density vector, \(\vec{J}\). The integral version states that the circulation of the magnetic field about a closed curve is equal to \(4\pi\) times the net electric current \(I\) through any surface whose boundary is the given closed curve.

1. Differential version:   \(\vec{\nabla}\times\vec{B}=4\pi\vec{J}\)
2. Integral version:   \(\displaystyle \oint_C \vec{B}\cdot d\vec{s}=4\pi I\)

\(C\) is a closed curve and \(S\) is any surface whose boundary is the curve \(C\). \(\vec{J}\) is the electric current density and \(I\) is the net electric current passing thru the surface \(S\) which can be computed from the integral \(\displaystyle I=\iint_S \vec{J}\cdot d\vec{S}\).

In the following example, we will use Ampere's Law to find the current \(I\) through a surface from the magnetic field \(\vec{B}\) in two different ways, once from the flux of the current density through a surface and once from a line integral about the boundary of the surface.

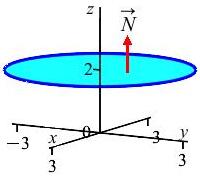
We first find \(\vec{J}\) using Ampere's law, then compute \(I\) as a flux integral.
To use the differential version of Ampere's law, we need to find the curl of \(\vec{B}\): \[\begin{aligned} \vec{\nabla}\times\vec{B} &=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \partial_x & \partial_y & \partial_z \\ -6y & 6x & 0 \end{vmatrix} \\ &=\hat{\imath}(0)-\hat{\jmath}(0)+\hat{k}(6+6) =\langle 0,0,12\rangle \end{aligned}\] By Ampere's Law, \[ \vec J=\dfrac{1}{4\pi} \vec{\nabla}\times\vec{B} =\dfrac{1}{4\pi}\langle 0,0,12\rangle =\left\langle 0,0,\dfrac{3}{\pi}\right\rangle. \] This is the current density at each point in space. To find the current, we compute the flux of the current density through the disk. To do that, we parameterize the disk as: \[ \vec{R}(r,\theta)=(r\cos\theta,r\sin\theta,2) \] Then we find the normal vector: \[\begin{aligned} \vec{N}&=\vec{e}_r\times\vec{e}_\theta= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \cos\theta & \sin\theta & 0 \\ -r\sin\theta & r\cos\theta & 0 \end{vmatrix} \\ &=\hat{\imath}(0)-\hat{\jmath}(0)+\hat{k}(r) =\langle 0,0,r\rangle \end{aligned}\] This correctly points upward. So, the current integral is computed as \[\begin{aligned} I&=\iint_S \vec{J}\cdot d\vec{S} =\iint \left\langle 0,0,\dfrac{3}{\pi}\right\rangle \cdot\langle 0,0,r\rangle\,dr\,d\theta =\int_0^{2\pi}\int_0^3 \dfrac{3}{\pi}r\,dr\,d\theta\\ &=\dfrac{3}{\pi}(2\pi)\left[\dfrac{r^2}{2}\right]_0^3 =6\left(\dfrac{9}{2}\right)=27 \end{aligned}\]

Alternatively, use Ampere's Law to find \(\displaystyle I=\dfrac{1}{4\pi} \oint_C \vec{B}\cdot d\vec{s}\).
To do this, we parameterize the curve and find the velocity vector: \[ \vec{r}(\theta)=(3\cos\theta, 3\sin\theta, 2) \qquad \text{for} \quad 0 \lt \theta \lt 2\pi \] \[ \vec{v}(\theta)=\langle-3\sin\theta, 3\cos\theta, 0\rangle \] This correctly points counterclockwise. Also, we evaluate the magnetic field \(\vec{B}\) along the curve: \[ \vec{B}(\vec{r}(\theta)) =\langle-6y, 6x, 0\rangle =\langle-18\sin\theta,18\cos\theta, 0\rangle \] We can now compute the current as the line integral: \[\begin{aligned} I&=\dfrac{1}{4\pi} \oint_C \vec{B}\cdot d\vec{s} =\dfrac{1}{4\pi} \oint \vec{B}\cdot\vec{v}\,d\theta\\ &=\dfrac{1}{4\pi} \int_0^{2\pi} (54\sin^2\theta+54\cos^2\theta)\,d\theta =\dfrac{54}{4\pi} \int_0^{2\pi} \,d\theta=27 \end{aligned}\] This agrees with our other method of calculating \(I\)!

Although both methods of calculating the current returned the same answer, the line integral was simplier in this problem. The surface integral is easier in the next exercise.

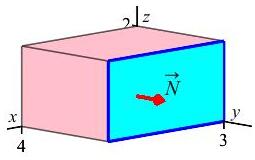
1. Find the current using a surface integral.

   The curent is the surface integral of the current density over the face.

   \(\displaystyle I=\iint_S \vec{J}\cdot d\vec{S}=0\)

   The curent is the surface integral of the current density which is computed from the curl of the magnetic field. This is: \[\begin{aligned} \vec{\nabla}\times\vec{B} &=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \partial_x & \partial_y & \partial_z \\ 3x-2y+3z & 2x-2y+5z & 3x-4y-z \end{vmatrix} \\ &=\hat{\imath}(-4-5)-\hat{\jmath}(3-3)+\hat{k}(2+2) =\langle -9,0,4\rangle \end{aligned}\] By Ampere's Law: \[ \vec J=\dfrac{1}{4\pi} \vec{\nabla}\times\vec{B} =\dfrac{1}{4\pi}\langle -9,0,4\rangle =\left\langle \dfrac{-9}{4\pi},0,\dfrac{1}{\pi}\right\rangle \] The surface is the face \(y=3\) for \(0\le x\le4\) and \(0\le z\le2\) which may parametrized by \(\vec R=(x,3,z)\). We compute the normal: \[\begin{aligned} \vec{N}&=\vec{e}_x\times\vec{e}_z =\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{vmatrix} \\ &=\langle 0,-1,0\rangle \end{aligned}\] We need the surface oriented toward increasing \(y\). So we reverse the normal: \[ \vec{N}=\langle 0,1,0\rangle \] Then the current is the integral: \[\begin{aligned} I&=\iint_S \vec{J}\cdot d\vec{S} =\iint \left\langle \dfrac{-9}{4\pi},0,\dfrac{1}{\pi}\right\rangle \cdot\langle 0,1,0\rangle\,dx\,dz \\ &=\int_0^2\int_0^4 0\,dx\,dz =0 \end{aligned}\]

2. Find the current using a line integral.

   The curent is the line integral of the magnetic field around the boundary of the face.

   \(\displaystyle I=\dfrac{1}{4\pi} \oint_C \vec{B}\cdot d\vec{s}=0\)

   The curent is the line integral of the magnetic field around the boundary of the face which consists of \(4\) line segments traversed counterclockwise as seen from the positive \(y\)-axis. Their parametrizations, parameter ranges and tangent vectors are computed here along with a notation of which edges need to be reversed.
   (The plot shows the direction of each parametrization, but \(\vec r_1\) and \(\vec r_4\) need to be reversed to go counterclockwise.)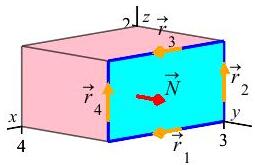

   

   \[\begin{aligned} \vec r_1&=\langle x,3,0\rangle &0&\le x\le 4 &\vec v_1&=\langle 1,0,0\rangle &&\text{reverse} \\ \vec r_2&=\langle 0,3,z\rangle &0&\le z\le 2 &\vec v_2&=\langle 0,0,1\rangle && \\ \vec r_3&=\langle x,3,2\rangle &0&\le x\le 4 &\vec v_3&=\langle 1,0,0\rangle && \\ \vec r_4&=\langle 4,3,z\rangle &0&\le z\le 2 &\vec v_4&=\langle 0,0,1\rangle &&\text{reverse} \end{aligned}\] We will implement the reversals by including a minus when we add the integrals. The magnetic fields, \(\vec{B}=\langle 3x-2y+3z, 2x-2y+5z, 3x-4y-z\rangle\), on each curve and their dot products with the velocities are: \[\begin{aligned} \vec B(\vec r_1)&=\langle 3x-6, 2x-6, 3x-12\rangle &\vec B\cdot\vec v_1&=3x-6 \\ \vec B(\vec r_2)&=\langle -6+3z, -6+5z, -12-z\rangle &\vec B\cdot\vec v_2&=-12-z \\ \vec B(\vec r_3)&=\langle 3x, 2x+4, 3x-14\rangle &\vec B\cdot\vec v_3&=3x \\ \vec B(\vec r_4)&=\langle 6+3z, 2+5z, -z\rangle &\vec B\cdot\vec v_4&=-z \end{aligned}\] Then the \(4\) line integrals are: \[\begin{aligned} \int_{\vec r_1} \vec B\cdot d\vec s&=\int_0^4 3x-6\,dx=\left[\dfrac{3x^2}{2}-6x\right]_0^4=0 \\ \int_{\vec r_2} \vec B\cdot d\vec s&=\int_0^2 -12-z\,dz=\left[-12z-\dfrac{z^2}{2}\right]_0^2=-26 \\ \int_{\vec r_3} \vec B\cdot d\vec s&=\int_0^4 3x\,dx=\left[\dfrac{3x^2}{2}\right]_0^4=24 \\ \int_{\vec r_4} \vec B\cdot d\vec s&=\int_0^2 -z\,dz=\left[-\dfrac{z^2}{2}\right]_0^2=-2 \end{aligned}\] Finally, taking into account the orientation reversals, the current is: \[\begin{aligned} I&=\dfrac{1}{4\pi} \oint_C \vec{B}\cdot d\vec{s} =\dfrac{1}{4\pi} \left[-\int_{\vec r_1}+\int_{\vec r_2}+\int_{\vec r_3}-\int_{\vec r_4}\right] \\ &=\dfrac{1}{4\pi} \left[0-26+24--2\right] =0 \end{aligned}\] Remarkable cancellations! But all that for \(0\)? Clearly, the surface integral was much easier since the current density \(\vec J\) was perpendicular to \(\vec N\) and the integrand was \(0\). However, in addition, there was only \(1\) surface integral while there were \(4\) line integrals and the orientations of the line segments were harder.